4. Redes Neuronales Convolucionales¶
En esta sección veremos las redes neuronales convolucionales, que son la herramienta más potente que existe a día de hoy para el procesado de imagen. Se utilizan en coches autónomos, en la búsqueda de imágenes de google, diagnóstico de enfermedades, interpretación del lenguaje, y muchas más aplicaciones.
La metodología de esta parte 2 será mediante realización autoguiada, y habrá que resolver la segunda parte para entregarla a través de la tarea habilitada en el campus virtual. El objetivo principal es implementar LeNet y entrenarla para los datos de MNIST.
Esta parte se compone de:
Una introducción a las redes neuronales convolucionales
Alexnet
Capas convolucionales
Max pooling
Realización práctica
Preparación de datos y librerías
Diseño de la red neuronal LeNet
Entrenamiento y test
4.1. Redes Neuronales Convolucionales¶
Tras el desarrollo del perceptrón en los años 80, las redes neuronales fueron algo marginal durante los años 90 y 2000s, debido en gran parte al desarrollo de nuevos modelos estadísticos para el reconocimiento de imágenes. Éstos eran igualmente potentes, pero se podían ejecutar en los PCs de la época, tardando relativamente poco en su entrenamiento.
En 2012, Alex Krizhevsky y Geoffrey Hinton ganaron el Imagenet Challenge, una competición online de clasificación de imágenes de más de mil categorías. Y lo hicieron con un error que era muy inferior a los demás competidores. Alexnet, la propuesta de los investigadores, era la única arquitectura que utilizaba redes neuronales en dicha competición, y utilizaba unos tipos de neuronas sobre los que apenas se había teorizado: las capas convolucionales. En el challenge de 2013 la mitad de los competidores usaban redes neuronales. Dos años después, apenas hubo algún competidor que usara otra estrategia.
Esto fue posible a lo que Nvidia denominó el Deep Learning Big Bang, una forma de llamar a la confluencia de tres características impensables décadas antes: una mayor capacidad de cómputo con la llegada de las GPU o tarjetas gráficas, que permitían ejecutar el código con un mayor grado de paralelismo junto una disponibilidad de datos sin precedentes gracias a internet y el Big Data. Esto permitía que las redes neuronales, que habían estado latentes durante décadas, se pudieran aplicar con resultados espectaculares. Hoy día, prácticamente todas las aplicaciones de inteligencia artificial son redes neuronales: desde coches autónomos hasta el traductor de Google; desde el sistema de recomendación de Spotify hasta la detección facial de Instagram. Y todo es gracias a Alexnet.
4.2. Alexnet¶
Alexnet no fue una propuesta especialmente novedosa. Utilizaba modelos de neuronas y capas que ya se habían teorizado en etapas anteriores. Pero las combinó de forma magistral y consiguió batir a todos sus competidores provenientes del aprendizaje estadístico. La red tiene dos partes bien diferenciadas: una compuesta por redes convolucionales y otra por redes densas. La primera realiza una extracción automática de características, mientras que la segunda es la parte propiamente de aprendizaje, o clasificación. Esta es la estructura de la red:

En la figura vemos varias palabras y elementos desconocidos:
Hay unos elementos en tres dimensiones (ortoedros) que tienen una anchura, altura y profundidad. Estos representan las capas convolucionales.
Hay otros elementos que son rectángulos en dos dimensiones: las capas densas, fully connected, o como las hemos visto en la parte anterior
nn.Linear.Entre cada capa aparece un rectángulo azul de diferente tamaño que conecta unas capas y otras. este es el reception field, o campo de recepción de una neurona convolucional.
Hay una interconexión entre capas convolucionales que se llama max pooling.
Aparece la palabra stride.
Con excepción de las capas densas, estos elementos son todavía desconocidos. Ahora nos adentraremos en el proceloso mundo de las arquitecturas convolucionales…
4.2.1. Capas Convolucionales¶
¿Qué son las capas convolucionales?, dices mientras clavas en mi pupila tu pupila azul…
Existe una tradición que considera las capas convolucionales como una arquitectura que realiza la convolución entre una imagen y un filtro. No es que sea errónea. Pero a los del procesado de señal nos hace pensar que realiza operaciones de alto nivel, cuando en realidad no son más que neuronas que hacen lo mismo que las de las capas lineales. Una neurona convolucional realiza la operación: $\( y_i^n = f(\mathbf{w^n}*\mathbf{y_{i}^{n-1}}+b_i^n)\)\( donde \)n\( es el número de capa (la capa de entrada es la 0), \)i\( el número de neurona dentro de cada capa y \)f()\( es una función de activación. **¿Os suena?** Es casi idéntico a la capa lineal. Solo que esta vez cambian los términos \)\mathbf{y_{i}^{n-1}}\( y \)\mathbf{w^n}$:
En el \(\mathbf{y_{i}^{n-1}}\) aparece un subíndice \(i\) que implica que, de alguna forma, para la neurona \(i\) de la capa \(n\) solo utilizaremos una parte de las salidas de la capa anterior. Concretamente una porción rectangular que conocemos como el reception field, el campo de recepción, también conocido como tamaño de kernel. Cada neurona convolucional sólo va a fijarse en ésa parte de la imagen (o de la salida de la capa) anterior. En general, siempre va a ser un número impar, por simplicidad.
En el \(\mathbf{w^n}\), sin embargo, ha desaparecido el subíndice \(i\). ¿Qué implica esto? Significa que la matriz de pesos es compartida por todas las neuronas de la capa \(n\), lo cual ahorra ingentes cantidades de memoria, y a la vez, es lo que hace que esta capa pueda realizar una convolución. Esa matriz de pesos también se conoce como filtros, y tendrá como tamaño
(F,W,H), dondeFes el “número de filtros”, yWyHel tamaño del filtro, que es el mismo que el tamaño de kernel. Visualmente, esta capa hace algo así:
Adicionalmente, las capas convolucionales tienen un parámetro que se llama stride, que hemos comentado anteriormente. Este parámetro es la distancia entre los reception field de las neuronas:
un valor
stride=1, indica que el centro de un reception field y el siguiente están a distancia 1 unidad.un valor
stride=2, indica que entre el centro de un reception field y el siguiente habrá 2 unidades de distanciaetc.
Cuanto mayor es el stride, menor será la superposición entre reception fields, y menor será el tamaño de la salida resultante de esa capa convolucional.
4.2.2. Max Pooling¶
Max pooling es una operación para reducir el tamaño de los mapas de salida. Para ello divide el mapa de entrada en reception fields de (W,H) con un determinado stride entre ellos y calcula el máximo de cada uno. El mapa resultante será el mapa que contiene los máximos de cada reception field. Por ejemplo, para un stride=2 y pooling=2, tenemos un mapa que se ha reducido a la mitad:

Con estas herramientas podemos ya diseñar nuestra propia Alexnet para clasificar números en MNIST.
4.3. Realización práctica¶
4.3.1. Preparación de librerías y datos:¶
En primer lugar vamos a importar pytorch, algunos módulos de la librería, y la librería de visualización matplotlib, como hicimos en la parte anterior:
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision.datasets as dset
import torchvision.transforms as transforms
from torchvision.utils import make_grid
import matplotlib.pyplot as plt
Vamos a crear el dataloader (cargador) de los datos de MNIST. Si hace falta se cargarán de nuevo, utilizando la utilidad torchvision.datasets y torch.utils.Dataloader. Posteriormente definiremos la función imshow() para mostrar un batch de los datos cargados. Todo este código es igual que el de la parte anterior.
trans = transforms.Compose([transforms.ToTensor()]) #Transformador para el dataset
root = './data/'
# definimos los conjuntos de training y test
train_set = dset.MNIST(root=root, train=True, transform=trans, download=True)
test_set = dset.MNIST(root=root, train=False, transform=trans, download=True)
batch_size = 128 # definimos el batchsize
# y creamos los dataloaders para training y testing
train_loader = torch.utils.data.DataLoader(
dataset=train_set,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(
dataset=test_set,
batch_size=batch_size,
shuffle=False)
# Y definimos de nuevo la función de mostrar un batch de los datos
def imshow(img):
img = img / 2 + 0.5 # desnormalizar
plt.imshow(img.permute(1, 2, 0))
# cambiamos las dimensiones para que el número de canales
# se muestre al final (por defecto en matplotlib)
# convertimos train_loader en un iterador
dataiter = iter(train_loader)
# y recuperamos el i-esimo elemento, un par de valores (imagenes, etiquetas)
images, labels = dataiter.next()
# Usamos la función imshow que hemos definido para mostrar imágenes
imshow(make_grid(images))

4.4. Diseño de la red neuronal¶
Ahora viene el meollo de la cuestión. Podríamos crear una red neuronal como una clase Alexnet. Sin embargo, este tipo de red requiere unas capacidades de computación que no todos tienen, y su entrenamiento está optimizado para su uso con GPU. En lugar de ello, vamos a utilizar una red llamada LeNet, que fue la precursora de Alexnet, y que tuvo un gran impacto también. Hay que tener en cuenta que el tamaño de las imágenes MNIST es 28x28 con 1 canal (escala de grises) mientras que el de Imagenet (la base de datos que usaba el Alexnet original) es de 224x224, y con 3 canales (RGB). La arquitectura de LeNet quedará:
conv1: Convolución sinstridey 6 filtros para un reception field de 5x5.Max-pooling de 2 sin
stride.conv2: Convolución sinstride, 16 filtros, reception field de 5x5.Max-pooling de 2 sin
stride.conv3: Convolución sin stride, 120 filtros, reception field de 3x3.Cambio a capas lineales (usar
tensor.view()).fc1: Capa densa (linear) de 256 neuronas.fc2: Capa densa (linear) de 10 neuronas.

Todas las capas convolucionales y densas utilizarán activación ReLU, salvo la última, que utilizará la función SoftMax, como en el perceptrón multicapa.
Aquí se listan los comandos utilizados para crear las diferentes capas:
Capa convolucional de 2 dimensiones:
nn.Conv2d(in_channels, out_channels, kernel_size, padding, stride=1).in_channelsserá el número de canales de entrada,out_channelsel número de canales de salida, que es lo mismo que el número de filtros,kernel_sizeserá el tamaño del kernel, o del reception field, que si es cuadrado basta con poner un entero igual al tamaño de un lado ystrideya lo conocéis. Elpaddinglo vamos a poner al entero inferior dekernel_size/2(asumiendo quekernel_sizesea impar), o sea, sikernel_sizees 3, pondremospadding=1, siks=5,padding=2, etc. Consulta aqui para profundizar sobre el padding.Max-pooling:
nn.MaxPool2d(kernel_size, stride=None).Y el resto, son
nn.Linear(), las funcionesF.relu()yF.softmax(), y el método.view()de los tensores de pytorch.
Si necesitas más detalles, te dejamos aquí una celda que utiliza la ayuda de jupyter. Esto es, escribiendo una función u objeto y añadiendo ? al final, y ejecutando. También puedes consultar la ayuda de pytorch.
nn.Conv2d?
x = images
x = model.conv1(x)
x = model.mp1(x)
x = model.conv2(x)
x.shape
torch.Size([16, 16, 14, 14])
Todavía hay que hacer un cálculo más, y es que para pasar de la útima capa convolucional a las capas fully-connected (nn.Linear()) tenemos que linealizar la salida de la capa. Si recordáis de la parte anterior, para una matriz x, esto se hace con x.view(tam_x,tam_y). Para este caso tenemos que usar x.view(-1, tam_y), donde tam_y será el tamaño del vector resultante de linealizar la salida de la capa conv3. Para ello tenemos que conocer, a priori, el tamaño que tendrá. ¿Y cual será ese tamaño?
Pues para conocerlo hay que propagar el tamaño. Si el batch size es BS, y las imagenes tienen tamaño (1,xx,yy) (en el caso de MNIST, (1,28,28)), la salida de conv1 será (BS,F1,xx,yy) siempre que hayáis utilizado el padding sugerido (el entero inferor a F1/2), con F1 el número de filtros de conv1 (en el caso sugerido, 6). Después pasa por un max_pooling, donde el tamaño se divide a la mitad, con lo que a la salida de mp1 nos queda un tamaño de (BS,F1,xx/2,yy/2). A la salida de conv2, tendremos (BS,F2,xx/2,yy/2), con F2 el número de filtros de conv2, y al pasar por el max pooling mp2, tendremos (BS,F2,xx/4,yy/4). Por último, al pasar por conv3, el tamaño de salida se convierte en (BS,F3,xx/4,yy/4). Así pues, como queremos llegar a un tamaño de (BS,L), con L el número de características totales para cada imagen, L será F3*xx/4*yy/4, o sea, F3*xx*yy/16.
Ahora, ya puedes implementar LeNet:
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__() # esta linea es siempre necesaria
self.conv1 = nn.Conv2d(1, 6, 5, padding=2)
self.mp1 = nn.MaxPool2d(2)
self.conv2 = nn.Conv2d(6, 16, 5, padding=2)
self.mp2 = nn.MaxPool2d(2)
self.conv3 = nn.Conv2d(16, 120, 3, padding=1)
self.fc1 = nn.Linear(7*7*120, 256)#capa oculta
self.fc2 = nn.Linear(256, 10)#capa de salida
def forward(self, x):
x = F.relu(self.conv1(x))
x = self.mp1(x)
x = F.relu(self.conv2(x))
x = self.mp2(x)
x = F.relu(self.conv3(x))
x = x.view(-1, 7*7*120)
x = F.relu(self.fc1(x))#Función de activación relu en la salida de la capa oculta
x = F.softmax(self.fc2(x), dim=1)#Función de activación softmax en la salida de la capa oculta
return x
Definimos el model, el loss y el optimizador, como en el caso anterior. Si queréis podéis probar otras variantes de optimizadores, como optim.Adam().
model = LeNet()
criterion = nn.CrossEntropyLoss() # definimos la pérdida
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
print(model)
LeNet(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(mp1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(mp2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(16, 120, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(fc1): Linear(in_features=5880, out_features=256, bias=True)
(fc2): Linear(in_features=256, out_features=10, bias=True)
)
Y a continuación vamos a entrenar el modelo. Os recomendamos utilizar unas 20 epochs como mínimo, aunque si va rápido en vuestro ordenador, podéis incrementar este número.
n_epochs = 20
for epoch in range(n_epochs):
print("Train") # Esta será la parte de entrenamiento
running_loss = 0.0 # el loss en cada epoch de entrenamiento
running_acc = 0.0 # el accuracy de cada epoch
total = 0
for i, (images, labels) in enumerate(train_loader, 0):
total += labels.shape[0]
# ponemos a cero todos los gradientes en todas las neuronas
optimizer.zero_grad()
# forward + backward + optimizar
outputs = model(images) # forward-pass
loss = criterion(outputs, labels) # evaluación del loss
loss.backward()# backward pass
optimizer.step() # optimización
# Mostramos las estadísticas
running_loss += loss.item() # acumulamos el loss de este batch
# extraemos las etiquetas que predice (nº neurona con máxima probabilidad)
_, predicted = torch.max(outputs, 1)
running_acc += torch.sum(predicted==labels) # y acumulamos el número de correctos
print(f'>>> Epoch {epoch} >>>> Loss: {running_loss/total}, Acc: {running_acc/total}')
Train
>>> Epoch 0 >>>> Loss: 0.01791902374426524, Acc: 0.22023333609104156
Train
>>> Epoch 1 >>>> Loss: 0.013324498097101848, Acc: 0.7682833075523376
Train
>>> Epoch 2 >>>> Loss: 0.012601996821165085, Acc: 0.8523333072662354
Train
>>> Epoch 3 >>>> Loss: 0.0124462657392025, Acc: 0.871233344078064
Train
>>> Epoch 4 >>>> Loss: 0.011892222328980764, Acc: 0.9433333277702332
Train
>>> Epoch 5 >>>> Loss: 0.011674345209201176, Acc: 0.9704499840736389
Train
>>> Epoch 6 >>>> Loss: 0.011635089653730392, Acc: 0.9747499823570251
Train
>>> Epoch 7 >>>> Loss: 0.011614095666011175, Acc: 0.9769333600997925
Train
>>> Epoch 8 >>>> Loss: 0.01159169866045316, Acc: 0.9796500205993652
Train
>>> Epoch 9 >>>> Loss: 0.011569740043083827, Acc: 0.9825999736785889
Train
>>> Epoch 10 >>>> Loss: 0.011556183155377707, Acc: 0.9839500188827515
Train
>>> Epoch 11 >>>> Loss: 0.011543800429503122, Acc: 0.9855999946594238
Train
>>> Epoch 12 >>>> Loss: 0.011533848734696706, Acc: 0.9868833422660828
Train
>>> Epoch 13 >>>> Loss: 0.011526075430711111, Acc: 0.9878333210945129
Train
>>> Epoch 14 >>>> Loss: 0.011521399462223053, Acc: 0.988183319568634
Train
>>> Epoch 15 >>>> Loss: 0.011515843131144841, Acc: 0.9891166687011719
Train
>>> Epoch 16 >>>> Loss: 0.011510863087574642, Acc: 0.9894833564758301
Train
>>> Epoch 17 >>>> Loss: 0.011502736872434615, Acc: 0.9904166460037231
Train
>>> Epoch 18 >>>> Loss: 0.011495884642998378, Acc: 0.9913166761398315
Train
>>> Epoch 19 >>>> Loss: 0.011498651460806529, Acc: 0.9910333156585693
Y ahora comprobamos la precisión de la red con los datos de test. Sigue los pasos detallados en comentarios.
correct = 0
total = 0
with torch.no_grad(): # hay que deshabilitar la propagación de gradiente
for images, labels in test_loader:
outputs = model(images) # forward pass
_, predicted = torch.max(outputs, 1) # estimación de etiquetas
total += labels.size(0)
correct += torch.sum(predicted == labels).item() # acumular el número de datos correctos.
print(f'Precisión del modelo en las imágenes de test: {correct / total}')
Precisión del modelo en las imágenes de test: 0.9886
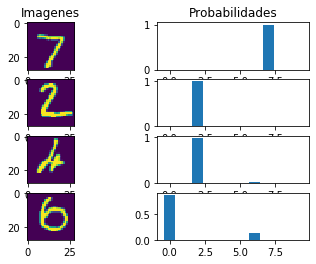
Si habéis entrenado por más de 20 epochs y todo está correcto, deberíais haber tenido una precisión muy alta, en torno al 98% (0.98). Esto, de por sí, ya es mejor que el perceptrón multicapa. Como en el caso anterior, es interesante ver donde se ha equivocado el modelo, así que utilizamos la misma función:
def muestra_predicciones(model, loader, n=2):
# numero de elementos de cada categoría a mostrar (nx2 total)
#init:
ncorrect=0
nwrong=0
# tamaño de los bloques.
size = (n,)+loader.dataset[0][0].shape
# este es el tamaño de la salida:
n_salida = list(model.children())[-1].out_features
# para almacenar los datos
im_correct_display = torch.empty(size)
im_wrong_display = torch.empty(size)
output_correct_display = torch.empty((n,n_salida))
output_wrong_display = torch.empty((n,n_salida))
with torch.no_grad(): # hay que deshabilitar la propagación de gradiente
for inputs, labels in loader:
outputs = model(inputs) # forward pass
_, predicted = torch.max(outputs, 1) # obtención de etiquetas numéricas
aciertos = predicted==labels
if sum(aciertos)>0 and ncorrect<n:
indices = torch.where(aciertos)[0] # obtiene los indices de los elementos correctamente clasificados
for i,ix in enumerate(indices[:n-ncorrect]):
im_correct_display[i+ncorrect] = inputs[ix]
output_correct_display[i+ncorrect] = outputs[ix]
ncorrect = ncorrect + i + 1
if sum(aciertos==False)>0 and nwrong<n:
indices = torch.where(aciertos==False)[0] # obtiene los indices de los elementos incorrectamente clasificados
for i,ix in enumerate(indices[:n-nwrong]):
im_wrong_display[i+nwrong] = inputs[ix]
output_wrong_display[i+nwrong] = outputs[ix]
nwrong = nwrong + i + 1
if ncorrect>=n and nwrong>=n:
break # si ya tenemos n correctos y n incorrectos, nos salimos
# Y ahora mostramos todos estos casos:
fig, ax = plt.subplots(n*2, 2) # esto crea un subplot de 4x2
for i in range(n):
ax[i][0].imshow(im_correct_display[i,0])
ax[i][1].bar(range(10),output_correct_display[i])
if i==0:
ax[i][0].set_title('Imagenes')
ax[i][1].set_title('Probabilidades')
ax[n+i][0].imshow(im_wrong_display[i,0])
ax[n+i][1].bar(range(10),output_wrong_display[i])
# y usamos la función:
muestra_predicciones(model, test_loader, n=2)
4.4.1. Otras alternativas:¶
Ahora os animo a probar otras configuraciones, cambiando los parámetros de la red, como tamaño y número de filtros, número de neuronas, o incluso probando otro tipo de optimizador (consulta las opciones disponibles en pytorch). Si te atreves -y tu ordenador puede-, puedes probar a añadir o quitar alguna capa. Cuenta tus impresiones acerca de qué ocurre al variar estos parámetros (si cambia la precisión máxima obtenida en test o la velocidad de convergencia -lo rápido que alcanza máxima precision-) n este recuadro:
Y esto es todo. Espero que os haya resultado útil. El mundo de las redes neuronales es enorme, y caben un millón de arquitecturas. En esta práctica solo pretendemos que conozcáis las herramientas que existen, y cómo se utilizan. A partir de aquí, el cielo es el límite!
